Programmierwettbewerb für
Schülerinnen und Schüler
Oktober 2025 – Juni 2026
Programmierwettbewerb für
Schülerinnen und Schüler
Oktober 2025 – Juni 2026
Im »Hidden Gems«-Wettbewerb müssen Gems, die an nicht vorhersehbaren Positionen auf dem Spielfeld zu nicht vorhersehbaren Zeiten (»ticks«) erscheinen, so rasch wie möglich eingesammelt werden. Je schneller der eigene Bot diese Positionen nacheinander erreicht, desto mehr Punkte landen auf seinem Konto (»score«).
Vor der Stage 2 »Dark Signal« wurden die Gem-Positionen unmittelbar bei ihrem Erscheinen mittels des JSON-strings angekündigt. Ab Stage 2 tauchen die Gems zwar auch in JSON-strings auf, aber erst, wenn sich der Bot dicht genug am Gem befindet. Ohne weitere Analyse läuft der Bot die meiste Zeit mehr oder weniger planlos herum, bis er zufällig in den Sichtbarkeitsbereich eines Gems gerät. So vergeht viel Zeit, bis der Bot weiß, wohin er tatsächlich zu laufen hat.
Als Ausgleich für diese beträchtliche Erschwerung senden die Gems nun in jedem Tick Signale aus, die vom Bot registriert werden. Die Signalstärke $A_i$, die der Bot vom Gem $i$ empfängt, hängt dabei vom aktuellen Abstand $d_i$ über die Beziehung
\begin{equation}
A_i = \displaystyle\frac{1}{1 + \displaystyle\frac{d_i^2}{r^2}} \qquad\qquad\qquad (1)
\end{equation}
ab, wobei $r$ ein bekannter konstanter Ausbreitungsradius ist. Mit abnehmender Entfernung zum Gem nimmt die Signalstärke somit zu und erreicht ihren Maximalwert 1, wenn der Bot den Gem erreicht hat ($d_i = 0$) und ihn einsammelt. Die Signalstärke wird dabei nicht durch zwischen Gem und Bot befindlichen Wänden (»walls«) beeinflusst. Als weitere Erschwerung werden die Signalstärken allerdings nicht für jeden sendenden Gem einzeln mitgeteilt, sondern nur als Summensignal, gerundet auf sechs Nachkommastellen. Senden zu einem Zeitpunkt $n$ Gems Signale aus, ergibt sich das Summensignal zu
\begin{equation}
A = \sum\limits_{i=1}^n A_i = \sum\limits_{i=1}^n \left(1 + \displaystyle\frac{d_i^2}{r^2}\right)^{-1}. \qquad (2)
\end{equation}
Somit ergibt sich eine Vielzahl von Möglichkeiten, aus welchen Einzelsignalen sich das Summensignal zusammensetzen kann. Auch ist nicht bekannt, wie viele Gems $(n)$ aktuell zu diesem Summensignal beitragen. Die Einzelsignalstärke (1) enthält keinerlei Information über die Richtung des eintreffenden Signals. Durch die Bewegung des Bots lässt sich aber die Quelle sehr rasch lokalisieren. Dazu wird für alle infrage kommenden Werte des Abstandsquadrates $d_i^2$ nicht nur dieser Wert herangezogen, sondern auch die beiden Verschiebungen $\Delta x$ und $\Delta y$, die ihn erzeugen:
\begin{equation}
d_i^2 = (\Delta x)^2 + (\Delta y)^2. \qquad\qquad\qquad (3)
\end{equation}
Die horizontalen und vertikalen Verschiebungen $\Delta x$ bzw. $\Delta y$, die vom Bot zum Gem führen, werden nachfolgend zu einem Zielvektor $[\Delta x, \Delta y]$ zusammengefasst. Die Komponenten des Vektors sind hier ganze Zahlen, wobei deren Vorzeichen und die Reihenfolge der beiden Summanden für das Abstandsquadrat selbst keine Rolle spielen, aber sehr wohl benötigt werden, um die Richtung eindeutig zu bestimmen.
Das Ziel dieses Blogs ist es, einen vom Autor entwickelten Algorithmus zu präsentieren, der ein Summensignal eindeutig in Einzelsignale zerlegt. Dadurch wird es möglich, einen neu auftauchenden Gem in möglichst kurzer Zeit zu lokalisieren. Alle Code-Beispiele sind in der Programmiersprache C++ angegeben. Die einzelnen Schritte werden nachfolgend erläutert. Da der Blog sehr lang wird und jeder Tag zählt für Teilnehmer:innen, die die Ideen in ihren Code einfließen lassen möchten, habe ich mich entschlossen, den Beitrag auf mehrere Teile aufzuteilen.
Da wir uns auf einem rechteckigen Spielfeld der Breite $w$ und der Höhe $h$ bewegen, wird jede Position $(x,y)$ mit $0 \le x \le w-1$ und $0 \le y \le h-1$ durch die Struktur point angegeben:
struct point {
int x; // x-Koordinate
int y; // y-Koordinate
point(void); // Konstruktor
point(int, int); // Konstruktor
float dist2(void); // Abstandsquadrat zum Ursprung
bool operator ==(const point&); // Gleichheit
};
point::point(void) { x = y = 0; }
point::point(int x0, int y0) { x = x0; y = y0; }
float point::dist2(void) { return (float)(x*x + y*y); }
bool point::operator ==(const point& p) { return (p.x == x && p.y == y) ? true : false; }
Die Struktur SgnLvl (»signal level«) beinhaltet die Einzelsignalstärken level$= A_i$ und der sie hervorrufende Zielvektor dist $= [\Delta x, \Delta y]$. Letzterer ist eine Variable vom Typ point, die eigentlich für Positionen (s. o.) gedacht ist, hier jedoch für einen (Verschiebungs-)Vektor genutzt wird.
struct SgnLvl {
float level = 0.0; // Signalstärke A_i
point dist; // Vektor zur Signalquelle
};
Um ein Summensignal eindeutig zerlegen zu können, brauchen wir natürlich eine Tabelle, die alle möglichen Signalstärken eines Einzelsignals auf dem Spielfeld auflistet. Dazu wird mithilfe der Funktion
float signal_level(point& p, const float& r)
{
float d2 = p.dist2();
return 1.0 / (1.0 + d2/(r*r));
}
die Signalstärke nach (1) berechnet. Der größte vorkommende Abstand verläuft diagonal über das Spielfeld, also $d^2_{\rm max} = (w-1)^2 + (h-1)^2$. Deshalb genügt es, eine Doppelschleife über alle möglichen Verschiebungen dx $= \Delta x$ und dy $= \Delta y$ abzuarbeiten, die alle Abstandsquadrate $d_i^2$ berechnet und sich die zugehörigen Zielvektoren merkt.
void calculate_signal_levels(const float& r)
{
point p;
int max, min, l = 0;
// bestimme die maximale und minimale Abmessung
if (HEIGHT >= WIDTH) {
max = HEIGHT;
min = WIDTH;
}
else {
max = WIDTH;
min = HEIGHT;
}
for (int dx = 0; dx < max; dx++) {
p.x = dx;
// i_min(dx, min) gibt das Minimum beider Parameter zurück
for (int dy = 0; dy < i_min(dx, min); dy++) {
// es gilt stets p.x >= p.y >= 0
p.y = dy;
SIGNAL_LVL[l].level = signal_level(p, r);
SIGNAL_LVL[l].dist = p;
l++;
}
}
NSIGNAL_LVL = l;
// sortiere die Signalstärken in aufsteigender Folge
bubble_sort();
}
Die gefundenen Signalstärken und Zielvektoren werden im globalen Array SIGNAL_LVL[] und deren Anzahl in der globalen Variablen NSIGNAL_LVL gespeichert. Beide werden im Hauptprogramm deklariert:
int NSIGNAL_LVL = 0; // Anzahl der berechneten Signalstärken
SgnLvl *SIGNAL_LVL = NULL; // Array mit den berechneten Signalstärken
...
SIGNAL_LVL = new SgnLvl[MAXLVL]; // Speicherplatz reservieren
Eine einfache Analyse ergibt, dass
als Größe des Arrays SIGNAL_LVL[] gerade ausreicht. Der Fall $\Delta x = \Delta y = 0$ wird dabei nicht erfasst, denn wenn der Bot auf dem Gem steht, piept er nicht länger. Damit die Einzelsignalstärken anschließend schnell aufgefunden werden, empfiehlt sich eine Sortierung nach aufsteigender Größe. Als Sortiermethode wird hier der Einfachheit halber »bubble sort« verwendet.
void swap_signal_levels(const int& i, const int& j)
{
float level = SIGNAL_LVL[i].level;
point p = SIGNAL_LVL[i].dist;
SIGNAL_LVL[i].level = SIGNAL_LVL[j].level;
SIGNAL_LVL[i].dist = SIGNAL_LVL[j].dist;
SIGNAL_LVL[j].level = level;
SIGNAL_LVL[j].dist = p;
}
void bubble_sort(void)
{
for (int i = NSIGNAL_LVL-1; i > 0; i--)
for (int j = 0; j < i; j++)
if (SIGNAL_LVL[j].level > SIGNAL_LVL[j+1].level)
swap_signal_levels(j, j+1);
}
Für die nachfolgenden Schritte wird vorausgesetzt, dass
Irgendwann taucht zum ersten Mal in einer Runde ein Signal auf. Dieses kann nur von einem einzelnen Gem stammen, die zugehörige Signalstärke muss somit im obigen Array SIGNAL_LVL[] verzeichnet sein. Dieses aufzufinden ist daher kein Problem. Komplizierter wird es, wenn sich bereits zwei Signale zu einer Summe addieren. Um die Historie aller vom Bot empfangenen Signale abzuspeichern, wird die Datenstruktur SgnEvn (»signal event«) benutzt:
struct SgnEvn {
int tick = -1; // Tick bei Erscheinen des Signals
float level = 0.0; // Summensignalstärke, die per JSON mitgeteilt wurde
point bot; // aktuelle Position des Bots
int nsrc = -1; // Anzahl der Einzelsignale dieses Signals
int ndist = -1; // Anzahl der aktuellen Zielvektoren zu den Signalquellen
point *dist = NULL; // Zeiger auf das Array der Zielvektoren
};
Im Hauptprogramm wird dazu Folgendes deklariert:
int NSIGNAL_EVENT = 0; // Anzahl aller registrierten Signale
SgnEvn *SIGNAL_EVENT = NULL; // Array mit allen registrierten Signalen
...
SIGNAL_EVENT = new SgnStr[MAXTICKS]; // Speicherplatz reservieren
for (int i = 0; i < MAXTICKS; i++)
SIGNAL_EVENT[i].dist = new point[80]; // max. 80 Zielvektoren für ein Summensignal
Wenn MAXTICKS Ticks pro Runde angekündigt sind, sollten dies als maximale Feldgröße für das Array SIGNAL_EVENT[] ausreichend sein. Ebenso sind 80 Zielvektoren zu den Quellorten eine sehr konservative Abschätzung, die keinen »memory allocation error« verursachen sollte.
Wir beschreiben nun, wie ein per JSON mitgeteiltes (Summen-)Signal verarbeitet wird. Dies geschieht in der Funktion get_signal_levels(lvl), die aufzufindende Signalstärke ist lvl:
void get_signal_levels(const float& lvl)
{
int nd = 0;
float sumlvl;
// durchsuche die Tabelle nach einer Einzelsignalquelle
for (int i = 0; i < NSIGNAL_LVL; i++) {
if (fabs((sumlvl = SIGNAL_LVL[i].level) - lvl) < 1e-6) {
// das Einzelsignal 'lvl' wurde gefunden
SIGNAL_EVENT[NSIGNAL_EVENT].nsrc = 1;
SIGNAL_EVENT[NSIGNAL_EVENT].dist[nd++] = SIGNAL_LVL[i].dist;
}
// Abbruch der Schleife, wenn Signalstärke wegen Sortierung zu groß ist
if (SIGNAL_LVL[i].level > lvl)
break;
}
SIGNAL_EVENT[NSIGNAL_EVENT].ndist = nd;
...
// Fortsetzung im Codefragment 17
Eine gesonderte Bemerkung verdient die richtige Verarbeitung der Fließkommazahlen vom Typ float, die für die Signalstärken verwendet werden. Laut IEEE 754 standard können Variablen dieses Typs 6-7 Dezimalstellen ohne Genauigkeitsverlust speichern. Da die Signalstärken vom »runner« auf 6 Nachkommastellen gerundet werden und von höchstens einigen wenigen Gems stammen, sollte es für einen »Treffer« genügen, wenn der Betrag der Differenz von Ist- und Zielwert kleiner als $10^{-6}$ ist.
Nun kommt es im Laufe einer Runde oft vor, dass nicht nur ein Zielvektor $[\Delta x, \Delta y]$ zu einer empfangenen Signalstärke gehört, sondern mehrere.
Dies erhöht selbstverständlich die Anzahl der infrage kommenden Quellorte. An dieser Stelle muss erwähnt werden, dass die bisher betrachteten Zielvektoren noch nicht tatsächlich zu den Gems führen. Sie sind eher als »Prototyp« – im Sinne einer Äquivalenzklasse – für mehrere, genaue Zielvektoren aufzufassen.
Während die Komponenten der Prototypen $[\Delta x, \Delta y]$ (für die stets $\Delta x \ge \Delta y \ge 0$ außer $\Delta x = \Delta y = 0$ gilt) in eckige Klammern gesetzt werden, schreiben wir die genauen Zielvektoren in runde Klammern.
Wie viel genaue Zielvektoren sind nun im Einzelnen möglich? Bei genauerer Betrachtung lassen sich drei Fälle unterscheiden:
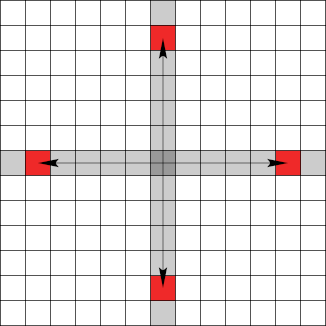
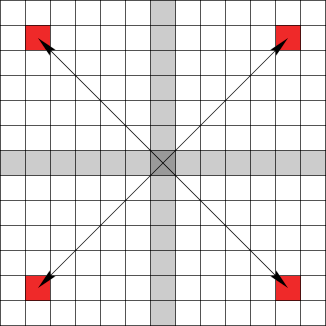
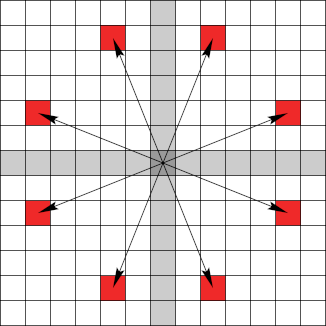
Im Teil 2 wird beschrieben, wie das Summensignal in Einzelsignale zerlegt wird, und wie nach einem oder zwei weiteren Ticks die Position des Gems zuverlässig festgestellt werden kann.